课程内容

《图形的平移》（1）
做一做
1、把图中的三角形ABC向右平移6格，画出所得到的三角形A′B′C′。
度量三角形ABC与三角形A′B′C′的边、角的大小，你发现了什么？
三角形ABC与三角形A′B′C′的对应边相等、对应角相等。
2、（1）下图是按照什么规律画出来的？
   （2）请按照这个规律继续画下去。
平移概念：在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移。
决定平移的两个要素：
（1）平移的方向；（2）平移的距离。
平移的特征：平移不改变图形的形状、大小。
议一议
1、平移图7-17（1），可以得到图7-17（2）（3）（4）中的哪一个图案？
2、图中的4个小三角形都是等边三角形，边长为1.3cm，你能通过平移三角形ABC得到其他三角形吗？若能，请画出平移的方向，并说出平移的距离。
3、如图是一幅”水兵合唱团“图案，说一说，这幅图案是如何运用平移制作的？
练习
1、平移改变的是图形的（   ）
   A、形状   B、位置   C、大小   D、形状、大小及位置
2、如图，∠DEF是∠ABC经过平移得到的，∠AB=33°，则∠DEF的度数为______。
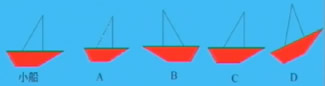
3、如图，小船平移得到的图形是：（   ）

4、将图中所示“箭头”向右平移6格，并向下平移5格，在方格中画出平移后的图形。并请说说你是怎么移的。
5、你知道线段CA的中点M以及线段BC上的点N平移到什么地方去了吗？请在图上标出它们的对应点M′和N′的位置。
6、如图，小船经过平移到了新的位置，你发现缺少什么了吗？请补上。
想一想
如图，长方形ABCD经过向右平移2厘米，向下平移3厘米后，再向_____平移_____厘米，向_____平移_____厘米就会与自身重合。
注意：
1、图形的平移是由移动的方向和距离决定的。
2、图形上各点沿同一方向移动相同的距离。
3、平移不改变图形的大小与形状，它只改变图形在平面中的位置。
课堂小结
今天我们学习了哪些知识呢？
平移概念：平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移。
决定平移的两个要素：
（1）平移的方向；（2）平移的距离。
平移的特征：平移不改变图形的形状、大小。