课程内容

《直线与圆的方程的应用》
例1：图中是某圆拱桥的一孔圆拱的示意图，该圆拱跨度AB=20m，拱高OP=4m，在建造时每隔4m需要用一个支柱支撑，求支柱A₂P₂的长度（精确到0.01）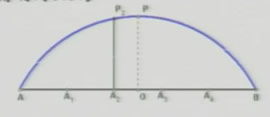

思考：（用坐标法）
1、圆心和半径能直接求出吗？
2、怎样求出圆的方程？
3、怎样求出支柱A₂P₂的长度？
例2：已经内接于圆的四边形的对角线互相垂直，求证圆心到一边的距离等于这条边所对边长的一半。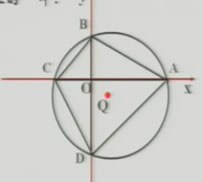

用坐标法解决平面几何问题的步骤：
第一步：建立适当的坐标系，用坐标和方程表示问题中的几何元素，将平面几何问题转化为代数问题；
第二步：通过代数运算，解决代数问题；
第三步：把代数运算结果“翻译”成几何结论。
练习：
1、等边△ABC点D、E分别在边BC、AC上，且|BD|=1/3|BC|，|CE|=1/3|CA|，AD、BE相交于点P，求证AP⊥CP。
2、求直线l：2x-y-2=0被圆C：（x-3）²+y²=0所截得的弦长。
3、某圆拱桥的水面跨度20m，拱高4m，现有一船，宽10m，水面以上高3m，这条船能否从桥下通过？
4、点M在圆心为C₁的方程：x²+y²+6x-2y+1=0，点N在圆心为C₂的方程：x²+y²+2x+4y+1=0，求|MN|的最大值。