课程内容
七年级数学上册第3章《有理数的运算》3.3 有理数的乘方(第一课时)
回答下列问题:
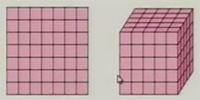
(1)怎样计算边长为7厘米的正方形的面积?
(2)怎样计算棱长为5厘米的立方体的体积?
为了简便,把7×7记作7²,5×5×5记作5³。
(-2)×(-2)×(-2)×(-2)×(-2)可以记作
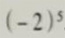
。
(-1/4)c×(-1/4)×(-1/4)×(-1/4)可以记作_______。
一般地,n个相同的因数a相乘,即
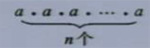
记作
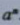
,求几个相同因数的积的运算,叫做乘方(power),乘方的结果叫做幂(power).在
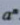
中,a叫做幂的底数(base number),n叫做幂的指数(exponent), 读作“a的n次方”,
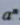
看做a的n次方的结果时,也可读作“a的n次幂”。
例:填空
(1)在5³中,底数是5,指数是3,读作5的3次方或5的立方。
(2)在
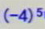
中,底数是-4,指数是5,读作-4的5次方或4的5次方的相反数。
一个数可以看作是这个数本身的1次方。例如3¹=3.
有理数的乘方运算通过有理数的乘法进行。
精讲点拨
例1.计算:
(1)(-4)³; (2)
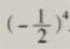
解:=(-4)×(-4)×(-4) =(-1/2)×(-1/2)×(-1/2)×(-1/2)
=-(4×4×4) =+(1/2×1/2×1/2×1/2)
=-64 =1/16
例2.计算:
(1)
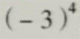
(2)
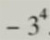
解:=(-3)×(-3)×(-3)×(-3) =-(3×3×3×3)
=+(3×3×3×3) =-81
=81
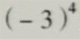
表示4个-3相乘。
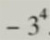
表示4个3相乘的相反数。
练习
1.填空
(1)在
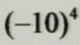
中,底数是-10,指数是4,运算的结果是10000。
(2)
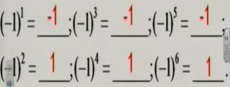
-1的奇次幂是-1.-1的偶次幂是1.
2.把下列各式写成乘方的形式;
(1)(-2/3)×(-2/3)×(-2/3)×(-2/3);
(2)2.5×2.5×2.5
3.计算
课堂小结
一般地,n个相同的因数a相乘,即
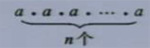
记作
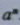
,求几个相同因数的积的运算,叫做乘方(power),乘方的结果叫做幂(power).在
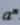
中,a叫做幂的底数(base number),n叫做幂的指数(exponent), 读作“a的n次方”,
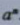
看做a的n次方的结果时,也可读作“a的n次幂”。
正数的任何次幂都是正数;负数的偶次幂是正数,负数的奇次幂是负数;0的正整数次幂都等于0.
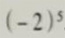 。
。 记作
记作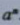 ,求几个相同因数的积的运算,叫做乘方(power),乘方的结果叫做幂(power).在
,求几个相同因数的积的运算,叫做乘方(power),乘方的结果叫做幂(power).在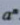 中,a叫做幂的底数(base number),n叫做幂的指数(exponent), 读作“a的n次方”,
中,a叫做幂的底数(base number),n叫做幂的指数(exponent), 读作“a的n次方”,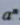 看做a的n次方的结果时,也可读作“a的n次幂”。
看做a的n次方的结果时,也可读作“a的n次幂”。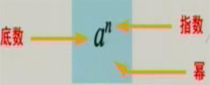
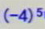 中,底数是-4,指数是5,读作-4的5次方或4的5次方的相反数。
中,底数是-4,指数是5,读作-4的5次方或4的5次方的相反数。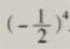
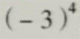 (2)
(2)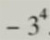
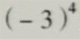 表示4个-3相乘。
表示4个-3相乘。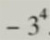 表示4个3相乘的相反数。
表示4个3相乘的相反数。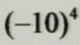 中,底数是-10,指数是4,运算的结果是10000。
中,底数是-10,指数是4,运算的结果是10000。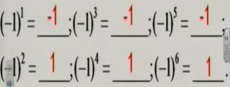

 记作
记作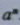 ,求几个相同因数的积的运算,叫做乘方(power),乘方的结果叫做幂(power).在
,求几个相同因数的积的运算,叫做乘方(power),乘方的结果叫做幂(power).在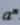 中,a叫做幂的底数(base number),n叫做幂的指数(exponent), 读作“a的n次方”,
中,a叫做幂的底数(base number),n叫做幂的指数(exponent), 读作“a的n次方”,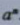 看做a的n次方的结果时,也可读作“a的n次幂”。
看做a的n次方的结果时,也可读作“a的n次幂”。