课程内容：

《平面向量的应用》
教学目标：
1.明确平面几何图形中的有关性质，如平移、全等、相似、长度、夹角等可以由向量的线性运算及数量积表示；
2.理解向量在处理平面几何问题中的优越性；
3.通过力的合成与分解模型、速度的合成与分解模型，掌握利用向量方法研究物理中相关问题的步骤，明了向量在物理中应用的基本题型，进一步加深对所学向量的概念和向量运算的认识；
4.通过对具体问题的探究解决，进一步培养学生的数学应用意识，提高应用数学的能力，体会数学在现实生活中的作用。
教学重点：
1.用向量方法解决实际问题的基本方法；
2.用向量解决几何问题的“三步曲”；
3.运用向量的有关知识对物理中的力、速度进行相关分析及计算。
教学难点：
1.如何将几何等实际问题化归为向量问题；
2.将物理中有关矢量问题转化为数学中向量问题。
复习：
1.两个向量的数量积；
2.平面两向量数量积的坐标表示；
3.向量平行于垂直的判定；
4.平面内两点间的距离公式；
5.求模：
例1.已知AC为⊙O的一条直径，∠ABC为圆周角。求证：∠ABC=90°。
例2.平行四边形是表示向量加法与减法的几何模型。如图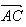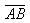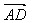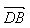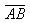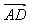，=+，=-，你能发现平行四边形对角线的长度与两条邻边长度之间的关系吗？
例3.如图，平行四边形ABCD中，点E、F分别是AD、DC边的中点，BE、BF分与AC交于R、T两点，你能发现AR、RT、TC之间的关系吗？
思考：运用向量方法解决平面几何问题可以分哪几个步骤？
“三步曲”：
（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；
（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题；
（3）把运算结果“翻译”成几何关系。
例4.如图，一条河的两岸平行，河的宽度d=500m，一艘船从A处出发到河对岸，已知船的速度v₁=10km/h，水流速度v₂=2km/h，问行驶航程最短时，所用时间时多少（精确到0.1min）？