课程内容
第22章《二次函数》22.1 二次函数的图象和性质(4)
学习目标:
会用描点法画出二次函数y=(x-h)2的图象,通过图象了解它们的图象特征和性质。
学习重点:
观察图象,得出上述二次函数的图象特征和性质。
1、复习二次函数y=ax2,y=ax2+k的图象和性质
(1)二次函数y=ax2,y=ax2+k的图象是什么?
(2)它们具有怎样的图象特征和性质?
(3)你是怎么研究的?
2、类比探究y=a(x-h)2的图象和性质
在同一直角坐标系中,画出二次函数y=- (x+1)2,y=-
(x+1)2,y=- (x-1)2的图象,并探究它们的图象特征和性质。
(x-1)2的图象,并探究它们的图象特征和性质。
探究:
画出二次函数y=- (x+1)2,y=-
(x+1)2,y=- (x-1)2的图象,并考虑它们的开口方向、对称轴和顶点。
(x-1)2的图象,并考虑它们的开口方向、对称轴和顶点。
| x |
… |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
y=- (x+1)2 (x+1)2 |
… |
-2 |
-1/2 |
0 |
-1/2 |
-2 |
-4.5 |
-8 |
… |
y=- (x-1)2 (x-1)2 |
… |
-8 |
-4.5 |
-2 |
-1/2 |
0 |
-1/2 |
-2 |
… |
可以看出,抛物线y=- (x+1)2的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,我们把它记作x=-1,顶点是(-1,0);抛物线y=-
(x+1)2的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,我们把它记作x=-1,顶点是(-1,0);抛物线y=- (x-1)2的开口向下,对称轴是x=1,顶点是(1,0)。
(x-1)2的开口向下,对称轴是x=1,顶点是(1,0)。
讨论:抛物线y=- (x+1)2,y=-
(x+1)2,y=- (x-1)2与抛物线y=-
(x-1)2与抛物线y=- x2有什么关系?
x2有什么关系?
归纳总结
二次函数y=a(x-h)2的图象是一条抛物线,它与抛物线y=ax2的形状相同,只是位置不同:它的对称轴是直线x=h,顶点坐标为(h,0)。
归纳:
一般地,当a>0时,抛物线y=a(x-h)2的对称轴是x=h,顶点是(h,0),开口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小。当x<h时,y随x的增大而减小,当x>h时,y随x的增大而增大。
抛物线y=- (x+1)2,y=-
(x+1)2,y=- (x-1)2与抛物线y=-
(x-1)2与抛物线y=- x2有什么关系?
x2有什么关系?
抛物线y=a(x-h)2与抛物线y=ax2有什么关系?
归纳:
当h>0时,把抛物线y=ax2向右平移h个单位长度,就得到抛物线y=a(x-h)2;
当h<0时,把y=ax2向左平移|h|个单位长度,就得到抛物线y=a(x-h)2。
本节重点:
当h>0时,把抛物线y=ax的平方向右平移h个单位长度,就得到抛物线y=a(x-h)的平方;
当h<0时,把y=ax的平方向左平移|h|个单位长度,就得到抛物线y=a(x-h)的平方。
张老师
女,中教高级职称
优秀教师,市级骨干教师、“教学标兵”、劳动模范,市数学教学与研究科研组带头人,注重教学改革与实践。
 (x+1)2,y=-
(x+1)2,y=- (x-1)2的图象,并探究它们的图象特征和性质。
(x-1)2的图象,并探究它们的图象特征和性质。 (x+1)2,y=-
(x+1)2,y=- (x-1)2的图象,并考虑它们的开口方向、对称轴和顶点。
(x-1)2的图象,并考虑它们的开口方向、对称轴和顶点。 (x+1)2
(x+1)2 (x-1)2
(x-1)2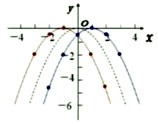
 (x+1)2的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,我们把它记作x=-1,顶点是(-1,0);抛物线y=-
(x+1)2的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,我们把它记作x=-1,顶点是(-1,0);抛物线y=- (x-1)2的开口向下,对称轴是x=1,顶点是(1,0)。
(x-1)2的开口向下,对称轴是x=1,顶点是(1,0)。 (x+1)2,y=-
(x+1)2,y=- (x-1)2与抛物线y=-
(x-1)2与抛物线y=- x2有什么关系?
x2有什么关系? (x+1)2,y=-
(x+1)2,y=- (x-1)2与抛物线y=-
(x-1)2与抛物线y=- x2有什么关系?
x2有什么关系?























