课程内容
第22章《二次函数》22.1 二次函数的图象和性质(5)
22.1.3 二次函数y=a(x-h)2+k的图象和性质
例3:(1)画出函数y=- (x+1)2-1的图象。
(x+1)2-1的图象。
解:作函数y=- (x+1)2-1的图象:
(x+1)2-1的图象:
| x |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
… |
y=- (x+1)2-1 (x+1)2-1 |
… |
-5.5 |
-3 |
-1.5 |
-1 |
-1.5 |
-3 |
-5.5 |
… |
(2)指出它的开口方向、对称轴及顶点。
(3)抛物线y=- x2经过怎样的变换可以得到抛物线y=-
x2经过怎样的变换可以得到抛物线y=- (x+1)2-1
(x+1)2-1
抛物线y=- (x+1)2-1的开口方向向下、对称轴是x=-1,顶点是(-1,-1)。
(x+1)2-1的开口方向向下、对称轴是x=-1,顶点是(-1,-1)。
归纳
一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同,把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k,平移的方向、距离要根据h,k的值来决定。
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点坐标是(h,k)。
练习
1、说出下列抛物线的开口方向、对称轴及顶点:
(1)y=2(x+3)2+5 (2)y=-3(x-1)2-2
(3)y=4(x-3)2+7 (4)y=-5(x+2)2-6
2、把抛物线y= x2-1先向右平移1个单位再向下平移2个单位,得到的抛物线的解析式为( )
x2-1先向右平移1个单位再向下平移2个单位,得到的抛物线的解析式为( )
A、y= (x-1)2-3 B、y=
(x-1)2-3 B、y= (x-1)2-3
(x-1)2-3
C、y= (x+1)2+1 D、y=
(x+1)2+1 D、y= (x+1)2-3
(x+1)2-3
例4:要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
解:如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点,因此可设这段抛物线对应的函数是
y=a(x-1)2+3(0≤x≤3)
由这段抛物线经过点(3,0)可得
0=a(3-1)2+3
解得 a=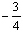
因此y=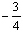 (x-1)2+3(0≤x≤3)
(x-1)2+3(0≤x≤3)
当x=0时,y=2.25,也就是说,水管应长2.25m。
本节重点:
一般地,抛物线y=a(x-h)的平方+k与y=ax的平方形状相同,位置不同,把抛物线y=ax的平方向上(下)向左(右)平移,可以得到抛物线y=a(x-h)的平方+k,平移的方向、距离要根据h,k的值来决定。
抛物线y=a(x-h)的平方+k有如下特点:
(1)当a>0时,开口向上;当a<0时,开口向下;
(2)对称轴是直线x=h;
(3)顶点坐标是(h,k)。
张老师
女,中教高级职称
优秀教师,市级骨干教师、“教学标兵”、劳动模范,市数学教学与研究科研组带头人,注重教学改革与实践。
 (x+1)2-1的图象。
(x+1)2-1的图象。 (x+1)2-1的图象:
(x+1)2-1的图象: (x+1)2-1
(x+1)2-1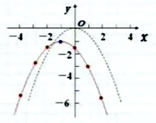
 x2经过怎样的变换可以得到抛物线y=-
x2经过怎样的变换可以得到抛物线y=- (x+1)2-1
(x+1)2-1 (x+1)2-1的开口方向向下、对称轴是x=-1,顶点是(-1,-1)。
(x+1)2-1的开口方向向下、对称轴是x=-1,顶点是(-1,-1)。 x2-1先向右平移1个单位再向下平移2个单位,得到的抛物线的解析式为( )
x2-1先向右平移1个单位再向下平移2个单位,得到的抛物线的解析式为( ) (x-1)2-3 B、y=
(x-1)2-3 B、y= (x-1)2-3
(x-1)2-3 (x+1)2+1 D、y=
(x+1)2+1 D、y= (x+1)2-3
(x+1)2-3
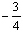 (x-1)2+3(0≤x≤3)
(x-1)2+3(0≤x≤3)























